Perudo Blog
I've known of this game since 2019. We used to play with cards instead of dice, which ended up removing much from the complexity of the game. Now, you can play with friends at perudoonline.com without owning a truly questionable number of dice.
A little about the game -- it's a survival game where you win by being the last player standing. Here are the rules if you want to learn more; they're also available on the website. See if you can come up with a strategy to beat your friends!
AI
(06-06-25) With some clever tricks, I've found one equilibrium (with many dominated strategies) for the 2 die vs 2 die game! The 2v2 player one payoff is -0.0168. In the 2v1 game, the player one payoff is 0.2748. In the 1v2 game, the payoff is -0.2716. The latter two results agree with other online computations, but as far as I know I am the only one to have solved the 2v2 game. My goal is to solve the 3 die vs 3 die game, but many more optimizations will need to be made. Then, I'll use these optimizations in the ones wild variant, and finally face off against dudo.ai (which only plays this variant.)
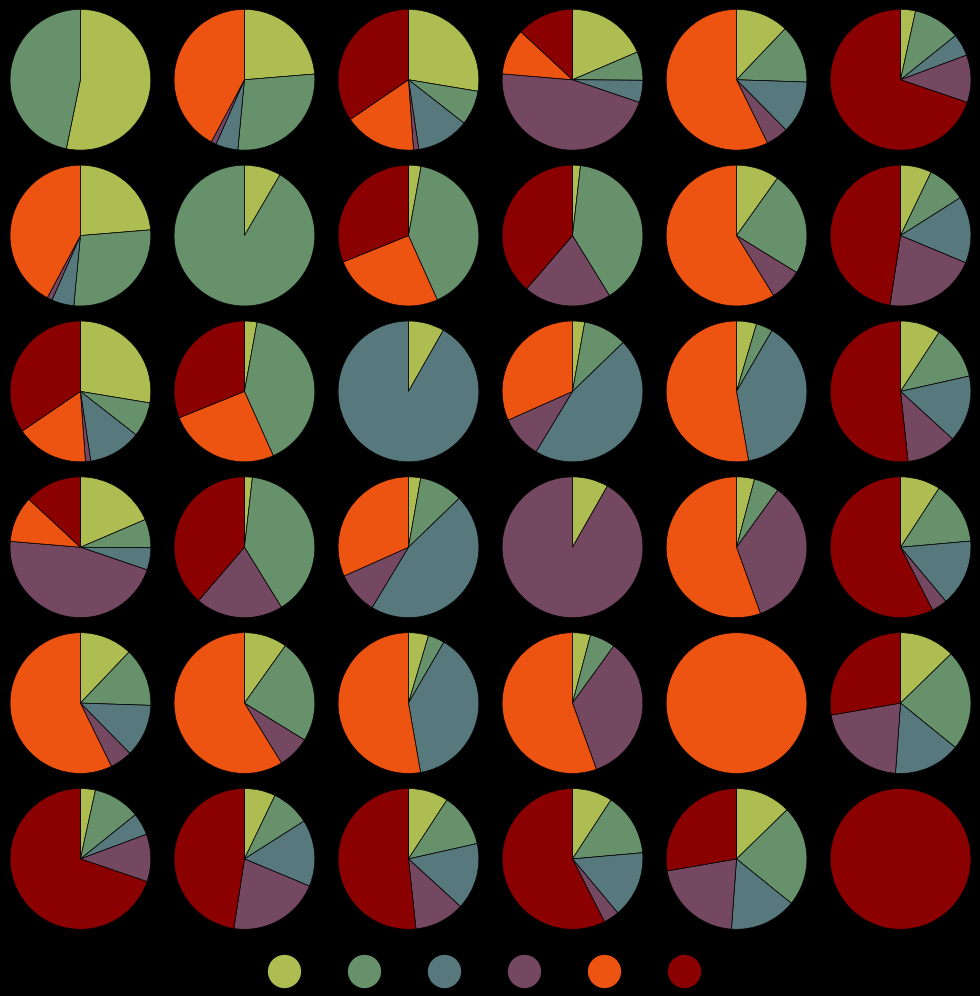
(06-05-25) Heads up, one die each. You roll a 4. Your opponent calls 2 3s. What is your best response?
Obviously, you should call BS. But there exists a nash equilibrium where you simply resign. I nodelocked my solver (some of it is on Github) to call BS, and the minimax payoff did not change -- which means that calling BS instead of resigning is also a nash equilibrium.
Why? To put it concisely, resigning is only weakly dominated by calling BS. And weakly dominated strategies may be a part of a nash equilibrium (NE). In this particular case -- if our opponent tries to exploit our resign, they will lose too much EV by calling 2 3s when we don't have a 4. So our opponent can't exploit our resign. The solver is very good at working in bad moves and working around them. The set of NE is not only trivially infinite, but also difficult to describe in its entirety. There are many situations where we can make clearly bad moves at cetain nodes of the game tree, and our opponent can't efficiently exploit them because they don't know what die we have. (If you've nodelocked with GTOWizard -- this is the same reason why GTOWizard will give you weird looking strategies at not-often-traversed-nodes of the game tree.) I've included the first move distribution for a particular equilibria: bluff iff you rolled a 1 or a 2.
(05-30-25) Perudo is just large enough to put naive LP-solving out of reach, as I found when I coded up a naive solution -- represent your strategy as a mix of all pure strategies, then iterate over opposing strategies and find a distribution that does well vs all of them. There are on the order of 12^(2^11) opposing pure strategies. Solution: use the Koller-Megiddo-Strengel algorithm that works with sequential representations of games.
I have to make some optimization choices, because the Koller algorithm as implemented on PyGambit doesn't exploit any nice properties and results in something like 12 hours of computation to solve the one vs one game. So I reimplemented the algorithm, adding simple optimizations like: when a matrix is guaranteed to be sparse, represent it as such. We've gotten to a 20000x speedup, and now we can solve the game in 2-3 seconds.
(01-13-25) My overall goal is to beat dudo.ai. The core idea is fine-tuning counter-factual regret techniques using pytorch, which is similar to experts. Thus far, I've ported some code to a collab notebook for CUDA (GPU) access, coded up a lot of utilities, and trained 2 models for a (measly) 6k iterations, varying a hyperparameter that I invented. As expected, one model simplifies strategies a little more aggressively than the other.
I've experimented with regret-hedge algorithms, including the one at https://arxiv.org/pdf/0903.2851 that tried to avoid the problem of tuning a learning rate parameter. However, when I implemented it, weighting weights in proportion to re^(r^2) empirically just converges poorly because the strategy "likes leaf nodes too much"
